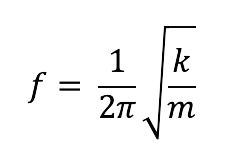
DYNAMIKA STRUKTURALNA – SZTYWNOŚĆ, MASA, TŁUMIENIE
REZONANS
Konstrukcje i maszyny często pracują w warunkach, gdzie są narażone na obciążenia dynamiczne. Z tego powodu, aby zapewnić długotrwałą i bezpieczną eksploatację części pojazdów, turbin, mostów czy budynków, na etapie projektowania powinna być uwzględniona ich charakterystyka dynamiczna.

Rotor maszyny wirującej
Zjawisko rezonansu, które zachodzi, gdy częstotliwość wzbudzenia struktury zrównuje się z częstotliwością drgań własnych obiektu, prowadzi do znacznego nasilenia się wibracji, które mogą doprowadzić do jego zniszczenia. Przykładem katastrofy spowodowanej rezonansem jest zawalenie się mostu wiszącego Tacoma w 1940 roku.

Most Tacoma w chwili zerwania
SZTYWNOŚĆ I MASA
Przykładowo, projektując wentylator przemysłowy, ważnym jest, aby częstotliwości drgań własnych wirnika nie pokrywały się z częstotliwością z jaką będzie się on obracał
w trakcie pracy. Z tego powodu kluczową staje się zdolność wpływania na częstotliwości rezonansowe konstrukcji. Wpływ parametrów układu na jego dynamikę można w prosty sposób przedstawić analizując model oscylatora harmonicznego o jednym stopniu swobody. Składa się on ze sprężyny, której jeden z końców jest utwierdzony, a na drugim przymocowana jest punktowo skupiona masa.
w trakcie pracy. Z tego powodu kluczową staje się zdolność wpływania na częstotliwości rezonansowe konstrukcji. Wpływ parametrów układu na jego dynamikę można w prosty sposób przedstawić analizując model oscylatora harmonicznego o jednym stopniu swobody. Składa się on ze sprężyny, której jeden z końców jest utwierdzony, a na drugim przymocowana jest punktowo skupiona masa.
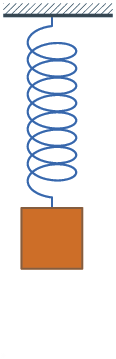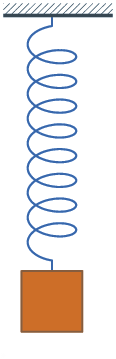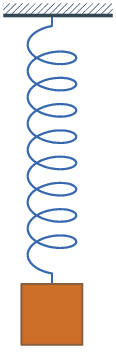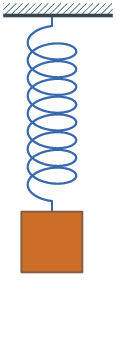
Oscylator harmoniczny o jednym stopniu swobody
Na podstawie tej zależności utworzono poniższe rysunki, które ukazują wpływ zmiany parametrów oscylatora harmonicznego na funkcję odpowiedzi częstotliwościowej (FRF – ang. Frequency Response Function). FRF jest funkcją w dziedzinie częstotliwości, która pokazuje jaki jest stosunek odpowiedzi układu do sygnału wejściowego. Piki na wykresie funkcji odpowiedzi częstotliwościowej pojawiające się dla konkretnych częstotliwości świadczą o tym, że występuje w niej zjawisko rezonansu. Na poniższych wykresach można zaobserwować jaki wpływ na częstotliwość rezonansową mają parametry układu takie jak sztywność i masa.
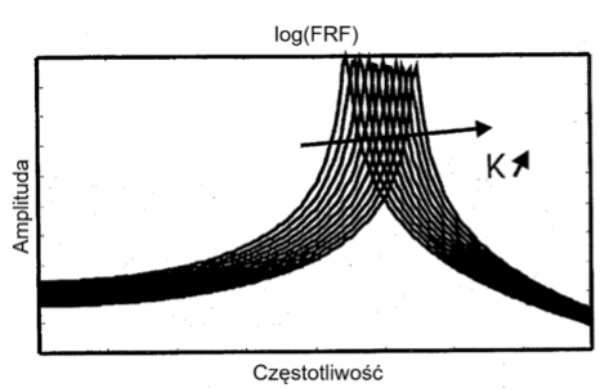
Zależność FRF układu od współczynnika sprężystości
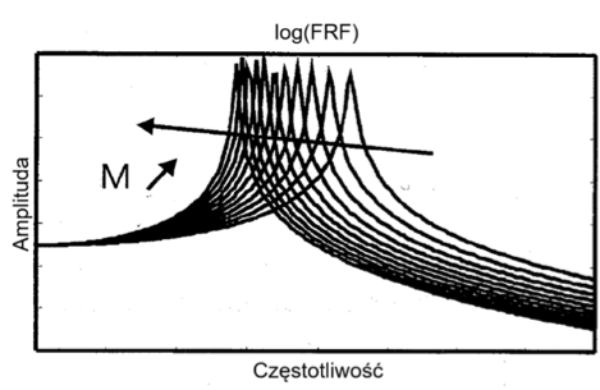
Zależność FRF układu od masy
W sytuacji, kiedy chcemy, aby konstrukcja pracowała w stanie podkrytycznym, na etapie projektu należy zadbać o to, żeby częstotliwości rezonansowe znajdowały się powyżej zakresu częstotliwości pracy. W celu zwiększenia częstotliwości drgań własnych konstrukcji należy zwiększyć jej współczynnik sprężystości lub zmniejszyć jej masę, co zazwyczaj stanowi dla inżynierów wyzwanie, żeby pomimo możliwie niewielkiej masy zachować wysoką sztywność struktury. Opisaną zależność otrzymaliśmy na podstawie analizy prostego układu o jednym stopniu swobody. Sprawdza się ona również w przypadku bardziej złożonych struktur o wielu stopniach swobody. Skutkuje to występowaniem wielu częstotliwości rezonansowych, w których struktura drga w odmienny sposób. Na poniższym rysunku znajduje się przykład belki jednostronnie utwierdzonej i jej pierwsze trzy postaci drgań, które odpowiadają pierwszym trzem częstotliwościom rezonansowym.
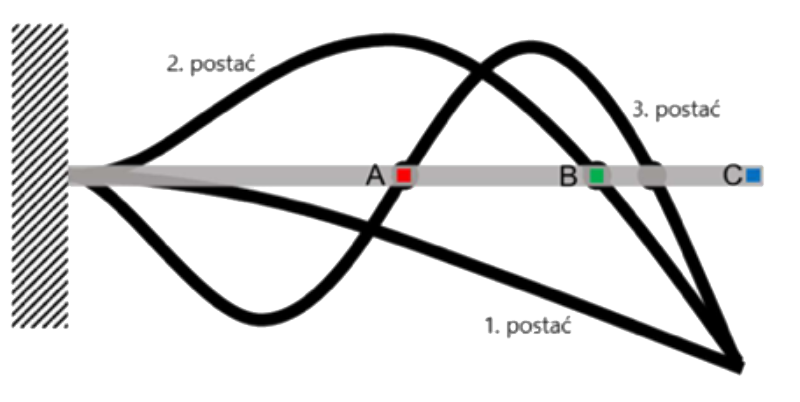
Postaci drgań własnych belki jednostronnie utwierdzonej
TŁUMIENIE
Tłumienie odpowiada za zmniejszanie się amplitudy drgań układu wraz z upływem czasu za sprawą rozpraszania energii. Z tego powodu stanowi ono ważny parametr konstrukcji mający wpływ na jej dynamiczne zachowanie.
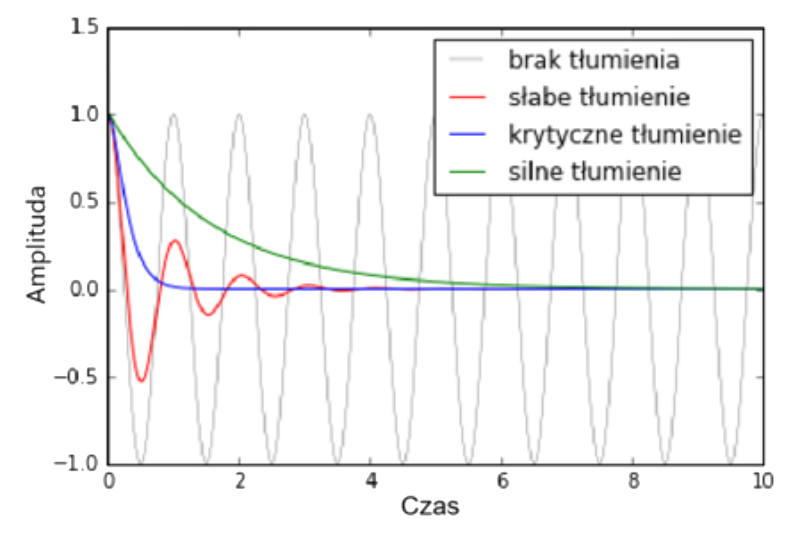
Drgania układu w zależności od tłumienia
Przeprowadzając analizę wpływu tłumienia na zachowanie układu w dziedzinie częstotliwości, można zauważyć, że wzrost tłumienia w nieznacznym stopniu wpływa na zmniejszenie częstotliwości rezonansowej. Tłumienie ma natomiast kluczowe znaczenie dla amplitudy, gdzie w przypadku rezonansu układu o niskim współczynniku tłumienia amplituda drgań znacząco wzrasta, co może stanowić zagrożenie dla bezpieczeństwa konstrukcji. Poniższy wykres przedstawia wpływ współczynnika tłumienia na amplitudę drgań rezonansowych.
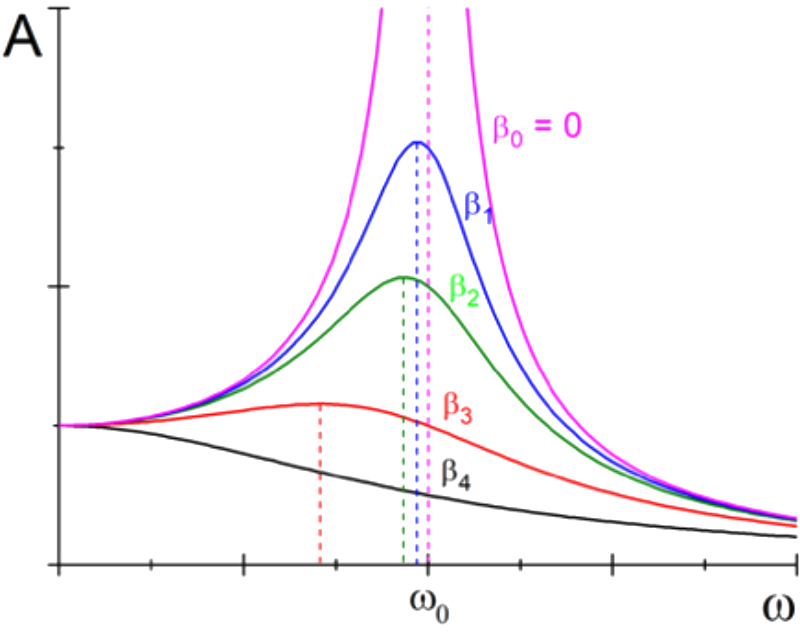
Krzywe rezonansu dla różnych wartości współczynnika
tłumienia β (β0 < β1 < β2 < β3 < β4)
tłumienia β (β0 < β1 < β2 < β3 < β4)
Wiedza na temat jak najskuteczniejszego tłumienia drgań jest kluczowa w przypadku projektowania np. zawieszenia samochodu. Odpowiednie wytłumienie nierówności drogi pozwala zapewnić jak najwyższy komfort podróży oraz bezpieczeństwo pokonywania zakrętów.
PODSUMOWANIE
Zjawiska związane z dynamiką strukturalną są obecne w codziennym życiu. Opisane w tym artykule zagadnienia stanowią jej teoretyczne podstawy. Dzięki ich zrozumieniu inżynierowie są w stanie uwzględnić aspekt dynamiki strukturalnej w trakcie projektowania konstrukcji, co często jest konieczne do zapewnienia ich bezpiecznej i niezawodnej pracy.
Jeśli jesteś zainteresowany realizacją kontroli testów jakości podczas produkcji, zachęcamy do kontaktu z firmą EC TEST Systems, która oferuje kompleksowe wsparcie w całym procesie wdrożenia systemu Simcenter Anovis